Samples

Random Number Generator

Here you can find a comparison between MCRand and Numpy for different probability distributions. Moreover, we use the program to generate random samples drawn from non-standard distributions.

To use the MCRand library to generate random numbers we first need to import the random generator (RandGen). This step can be done in the following way

from mcrand import sample

Gaussian distribution

To generate gaussian distributed numbers with the MCRand random generator we first need to define the Gaussian PDF

def gaussian(x, mu, sigma):
	return (1/(np.sqrt(2*np.pi*sigma**2))) * np.exp(-(x-mu)**2/(2*sigma**2))

Then, MCRand can be used to generate N gaussian numbers from x0 to xf as follows

x0 = -5
xf = 5
N = 1000

sigma = 1
mu = 0

gaussian_sample = sample(gaussian, x0, xf, N, mu, sigma)

Finally to plot the histogram and the PDF we can use matplotlib.pyplot

import matplotlib.pyplot as plt

plt.hist(gaussian_sample, bins=30, density=True, color=(0,1,0,0.5), label='MCRand sample')
plt.plot(x, gaussian(x, mu, sigma), color='r', label=r'Gaussian PDF $\mu=%.2f$, $\sigma=%.2f$' % (mu,sigma))

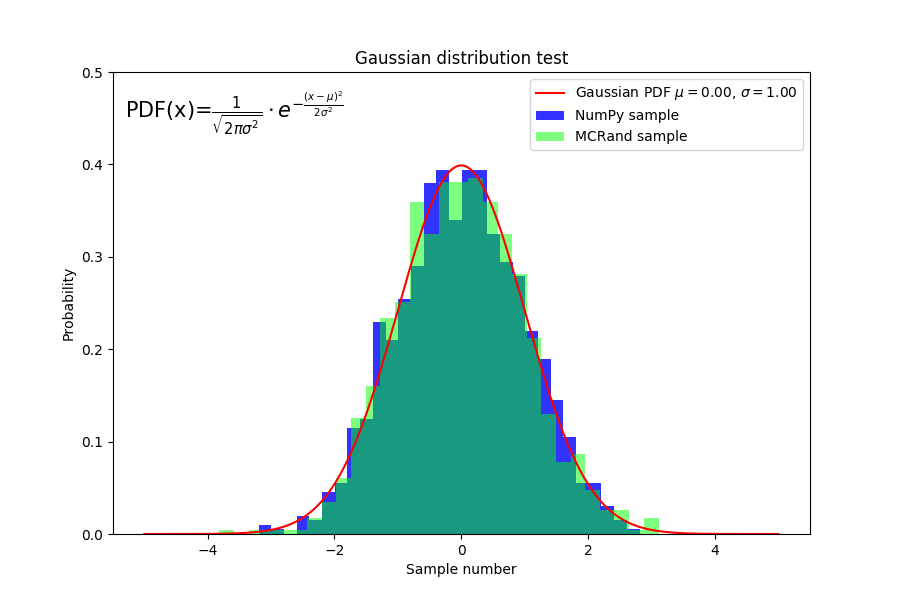Gaussian distribution with Numpy and MCRand

Cauchy distribution

To generate a Cauchy distribution we need to define its PDF

def cauchy(x, x0, gamma):
	return 1 / (np.pi * gamma * (1 + ((x-x0)/(gamma))**2))

and then use the random number generator of MCRand as before

x0 = -10
xf = 10
N = 10**5

x0_cauchy = 0
gamma = 1

cauchy_sample = sample(gaussian, x0, xf, N, mu, sigma)

Finally we plot the histogram and the PDF

plt.hist(cauchy_sample, bins=50, density=True, color=(0,1,0,0.5), label='MCRand sample')
plt.plot(x, cauchy(x, x0_cauchy, gamma), color='r', label=r'Cauchy PDF $\gamma=%.2f$, $x_0=%.2f$' % (gamma, x0_cauchy))

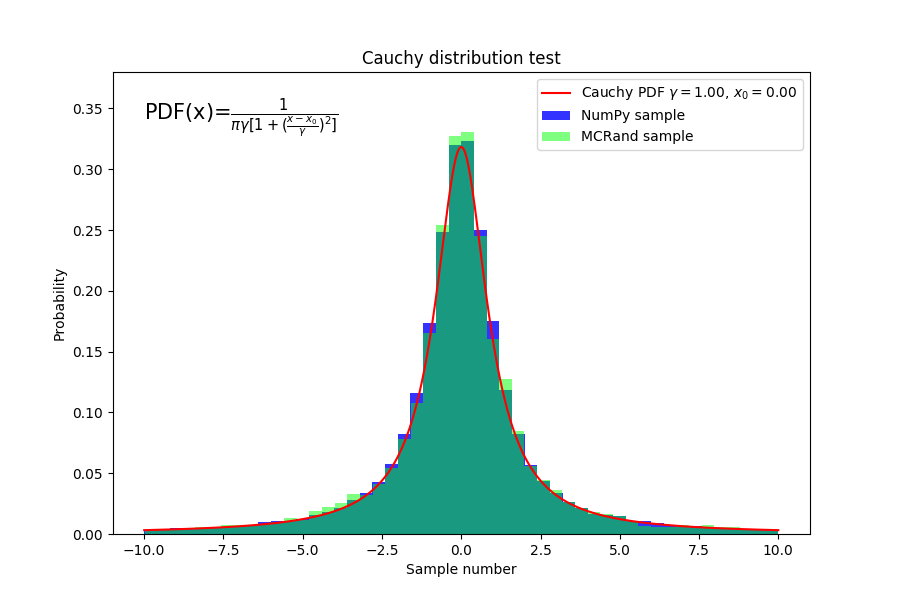Cauchy distribution with Numpy and MCRand

From now on, we’ll just write some code along with the output figures.

Exponential distribution

def exponential(x):
	return np.exp(-x)

x0 = 0
xf = 10
N = 10**5

rand = sample(exponential, x0, xf, N)

plt.hist(numpy_rand, bins=30, density=True, color=(0,0,1,0.8), label='NumPy sample')
plt.hist(rand, bins=30, density=True, color=(0,1,0,0.5), label='MCRand sample')

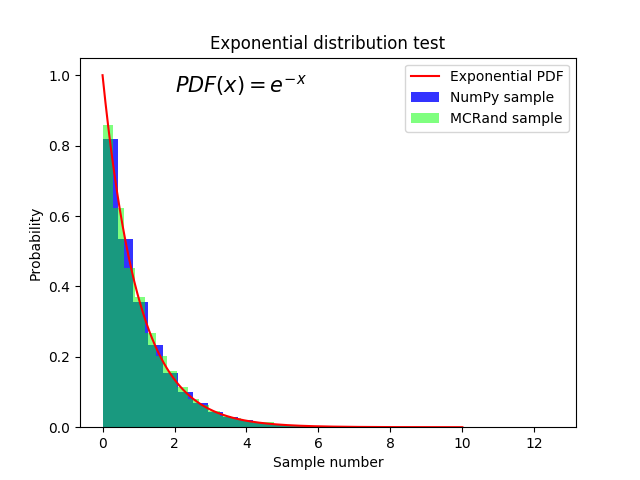Exponential distribution with Numpy and MCRand

Rayleigh distribution

def rayleigh(x, sigma):
	return (x*np.exp(-(x**2)/(2*sigma**2))) / (sigma**2)

x0 = 0
xf = 4
sigma = 1
N = 10**5

rand = sample(rayleigh, x0, xf, N, sigma)

plt.hist(rand, bins=30, density=True, color=(0,1,0,0.5), label='MCRand sample')
plt.plot(x, rayleigh(x, sigma), color='r', label=r'Rayleigh PDF $\sigma=%.2f$' % sigma)

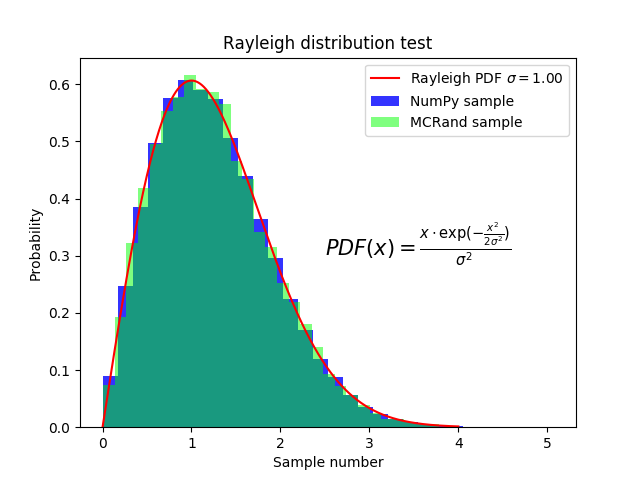Rayleigh distribution with Numpy and MCRand

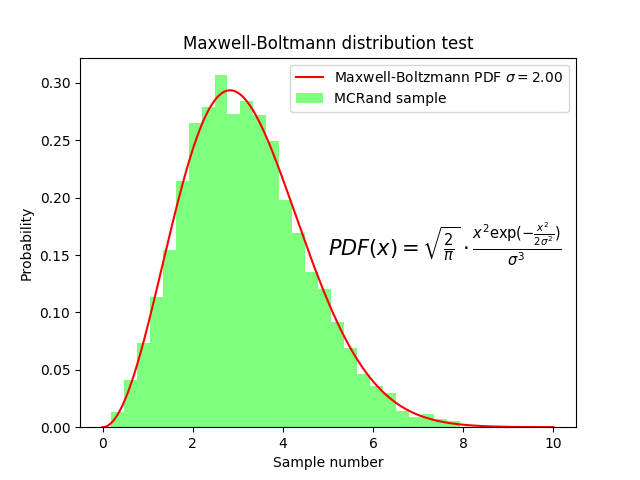
Maxwell-Boltzmann distribution

def maxwell_boltzmann(x, sigma):
	return (np.sqrt(2/np.pi))*(x**2*np.exp(-(x**2)/(2*sigma**2))) / (sigma**3)

x0 = 0
xf = 10
sigma = 2
N = 10**5

rand = sample(maxwell_boltzmann, x0, xf, N, sigma)

plt.hist(rand, bins=30, density=True, color=(0,1,0,0.5), label='MCRand sample')
plt.plot(x, maxwell_boltzmann(x, sigma), color='r', label=r'Maxwell-Boltzmann PDF $\sigma=%.2f$' % sigma)

Maxwell-Boltzmann distribution with Numpy and MCRand

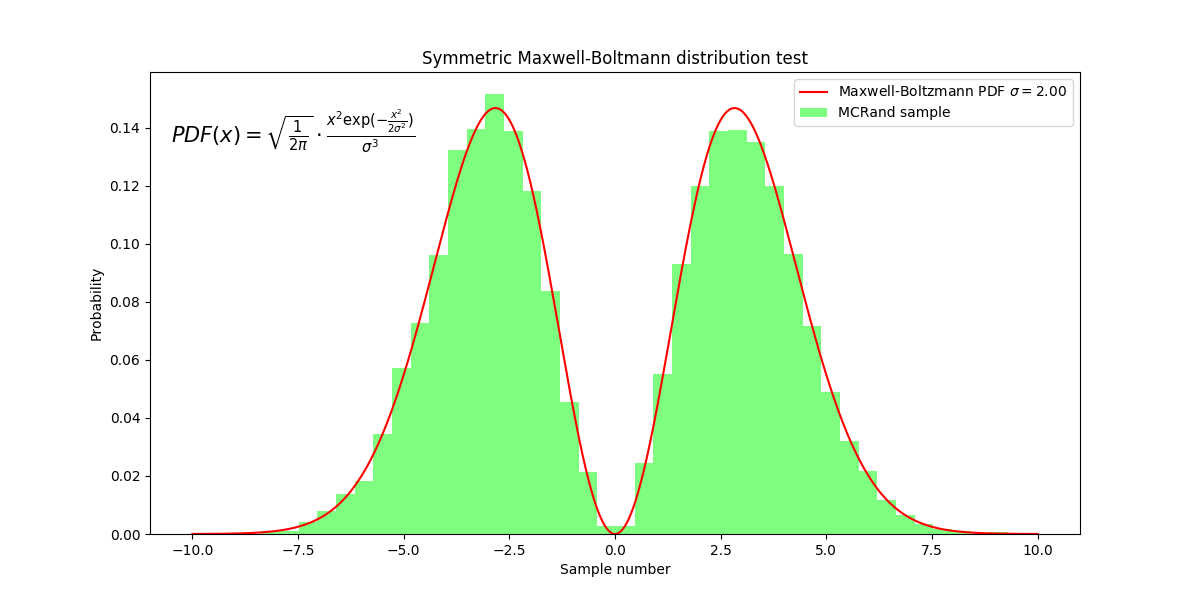
Symmetric Maxwell-Boltzmann distribution

def symmetric_maxwell_boltzmann(x, sigma):
	return 0.5*(np.sqrt(2/np.pi))*(x**2*np.exp(-(x**2)/(2*sigma**2))) / (sigma**3)

x0 = -10
xf = 10
sigma = 2
N = 10**5

rand = sample(symmetric_maxwell_boltzmann, x0, xf, N, sigma)

plt.hist(rand, bins=40, density=True, color=(0,1,0,0.5), label='MCRand sample')
plt.plot(x, symmetric_maxwell_boltzmann(x, sigma), color='r', label=r'Maxwell-Boltzmann PDF $\sigma=%.2f$' % sigma)

Symmetric Maxwell-Boltzmann distribution with Numpy and MCRand

Modified Rayleigh distribution

Finally we consider a invented probability distribution, given by the Rayleigh distribution multiplied by x. In some way we making a symmetric Rayleigh distribution. Then, this new distribution must be normalized, so the following equation must be acomplished:

equation

By nummeric integration it turns out that the normalization constant must be C=1/2.506628. Then we get the probability density function for this distribution.

Therefore, MCRand can be used to generate random numbers distributed following this distribution as follows

def invented(x, sigma):
	return (x**2*np.exp(-(x**2)/(2*sigma**2))) / (2.506628*sigma**2)

x0 = -4
xf = 4
sigma = 1
N = 10**5

rand = sample(invented, x0, xf, N, sigma)

plt.hist(rand, bins=40, density=True, color=(0,1,0,0.5), label='MCRand sample')
plt.plot(x, invented(x, sigma), color='r', label=r'Modified Rayleigh PDF $\sigma=%.2f$' % sigma)

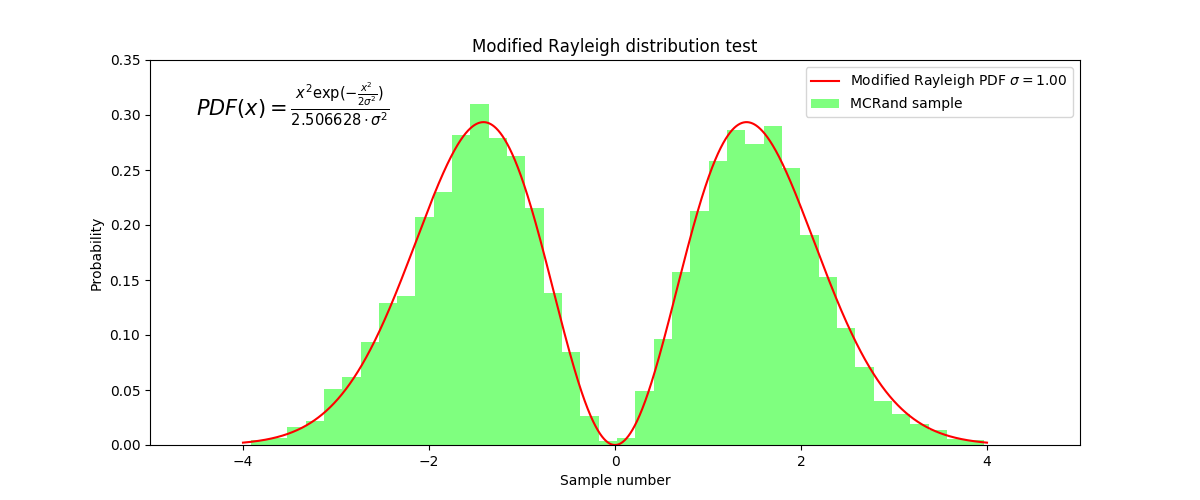Modified Rayleigh distribution with Numpy and MCRand

Multidimensional Integration

To use the MCRand library to perform multidimensional integrals we first need to import the Integrate module. This step can be done in the following way

from mcrand import uniform_integration

Then, we must define the function to integrate in an NumPy ndarray supported way, so it must be defined generally. For instance let’s imagine we want so solve the following integral:

equation

Then we should define the function as

def func(x):
	return np.sum(np.power(x, 2))

so each element of the x array will represent a variable.

Finally, to get the result with its error we can run the following code

x0 = [0, 0]
xf = [2, 3]
N = 10**6

result = uniform_integration(func, x0, xf, N)

print(result)

The result is given in the following format

(25.99767534344232, 0.02023068196284685)